Flow in a swale
Jump to navigation
Jump to search
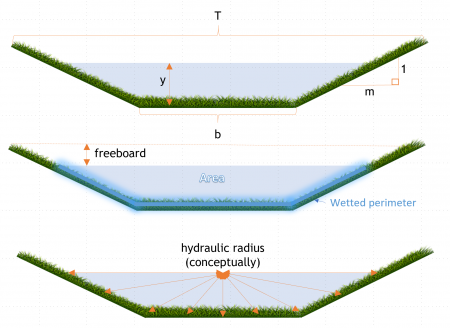
Where:
- Q = the flow in the swale (m3/s)
- A = the cross sectional area of the swale (m2)
- P = the wetted perimeter of the swale (m)
- S = the longitudinal slope (m/m)
- n = Manning's coefficient or 'Manning's n' (dimensionless)
| n value range | Good condition turf grass | Other |
|---|---|---|
| 0.002 - 0.010 | Where the average depth of flow is at ≥ 2 times the height of the vegetation | Supple tree seedlings such as willow or cottonwood growing where the average depth of flow is at ≥ 3 times the height of the vegetation |
| 0.010 - 0.025 | Where the average depth of flow is between 1 - 2 times the height of the vegetation | Moderately dense weeds, or tree seedlings growing where the average depth of flow is from 2 -3 times the height of the vegetation |
| 0.025 - 0.050 | Where the average depth of flow is about equal to the height of the vegetation | 8- to 10-year-old willow or cottonwood trees inter-grown with some weeds and brush (none of the vegetation in foliage) |
| 0.050 - 0.100 | Where the average depth of flow is < 0.5 times height of the vegetation | bushy willow trees about 1 year old inter-grown with weeds along side slopes (all vegetation in full foliage) |
References[edit]
- ↑ Arcement, G.J., Schneider, R. Guide for Selecting Manning's Roughness Coefficients for Natural Channels and Flood Plains U.S.G.S. WATER-SUPPLY PAPER 2339, 1989 https://pubs.usgs.gov/wsp/2339/report.pdf

